La demostración y comprobación experimental, en el laboratorio virtual, de las siguientes cuestiones referentes al péndulo simple:

1:- Para ángulos muy pequeños, un ángulo en radianes es igual que el seno de ese ángulo

R= La ecuación de un M.A.S. es

x=A·sen(ωt+φ)

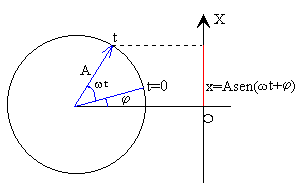En la figura, se observa la interpretación de un M.A.S. como proyección sobre el eje X, del extremo de un vector rotatorio de longitud igual a la amplitud A, que gira con velocidad angular w igual a la frecuencia angular del M.A.S, en el sentido contrario a las agujas del reloj.

El ángulo w t+j que forma el vector rotatorio con el eje de las X se denomina fase del movimiento. El ángulo j que forma en el instante t=0, se denomina fase inicial.

Eso quiere decir que un ángulo en radianes es igual que el seno de ese ángulo

 2:- Que el movimiento del péndulo simple es un MAS ¿Cual es la fuerza recuperadora, y su relación con la elongación?

R=

Se introduce

• la amplitud A, en el control de edición titulado Amplitud
• la frecuencia angular ω, en el control de edición titulado Frecuencia angular
• la fase inicial φ (en grados), en el control de edición titulado Fase inicial

Se pulsa en el botón titulado Empieza,

Para practicar con el programa interactivo, se sugiere probar los siguientes ejemplos:

Amplitud	Frecuencia	Fase inicial
2	1	0
2	1	90
2	1	180
2	1	270
2	2	0
1

 3:- Que la gráfica de elongación, velocidad y aceleración frente al tiempo es sinusoidal

R= Supongamos dos MAS de distinta frecuencia angular y con la misma fase inicial

x₁=A₁·sen(w₁·t)
x₂=A₂·sen(w₂·t)

De acuerdo con la interpretación geométrica de un MAS.

• El primer MAS es la proyección sobre el eje X de un vector de longitud A₁ que gira con velocidad angular w₁.
• El segundo MAS es la proyección sobre el eje X de un vector de longitud A₂ que gira con velocidad angular w₂.
• El MAS resultante es la proyección sobre el eje X del vector suma vectorial de los dos vectores.

De forma vectorial lo expresamos como El módulo del vector resultante no tiene una longitud constante su valor máximo es A1+A2 y su valor mínimo es ½A1-A2½ . Se dice entonces que la amplitud es modulada.

Cuando las amplitudes A₁=A₂ podemos expresar de forma más simple el MAS resultante

x= x₁+ x₂=A₁·sen(w₁·t)+A₁·sen(w₂·t)

Esta ecuación nos dice que se trata de un MAS de frecuencia angular (w₁+w₂)/2 y de amplitud

En la figura, en color rojo se muestra la amplitud modulada A y en color azul el resultado x de la composición de los dos MAS.

 

 4:- Que la Energía Mecánica no varía con el tiempo y su relación con la Cinética y la Potencial

R=

 

 

5:- Que el periodo varía con la longitud del hilo del péndulo

R=

 

 

6:- Que el periodo varía con la aceleración de la gravedad. Hacer comparación entre la Tierra y la luna. Aplicaciones prácticas en otras ramas de la Ciencia.

R=